Рисование геометрических тел. Рисование призмы

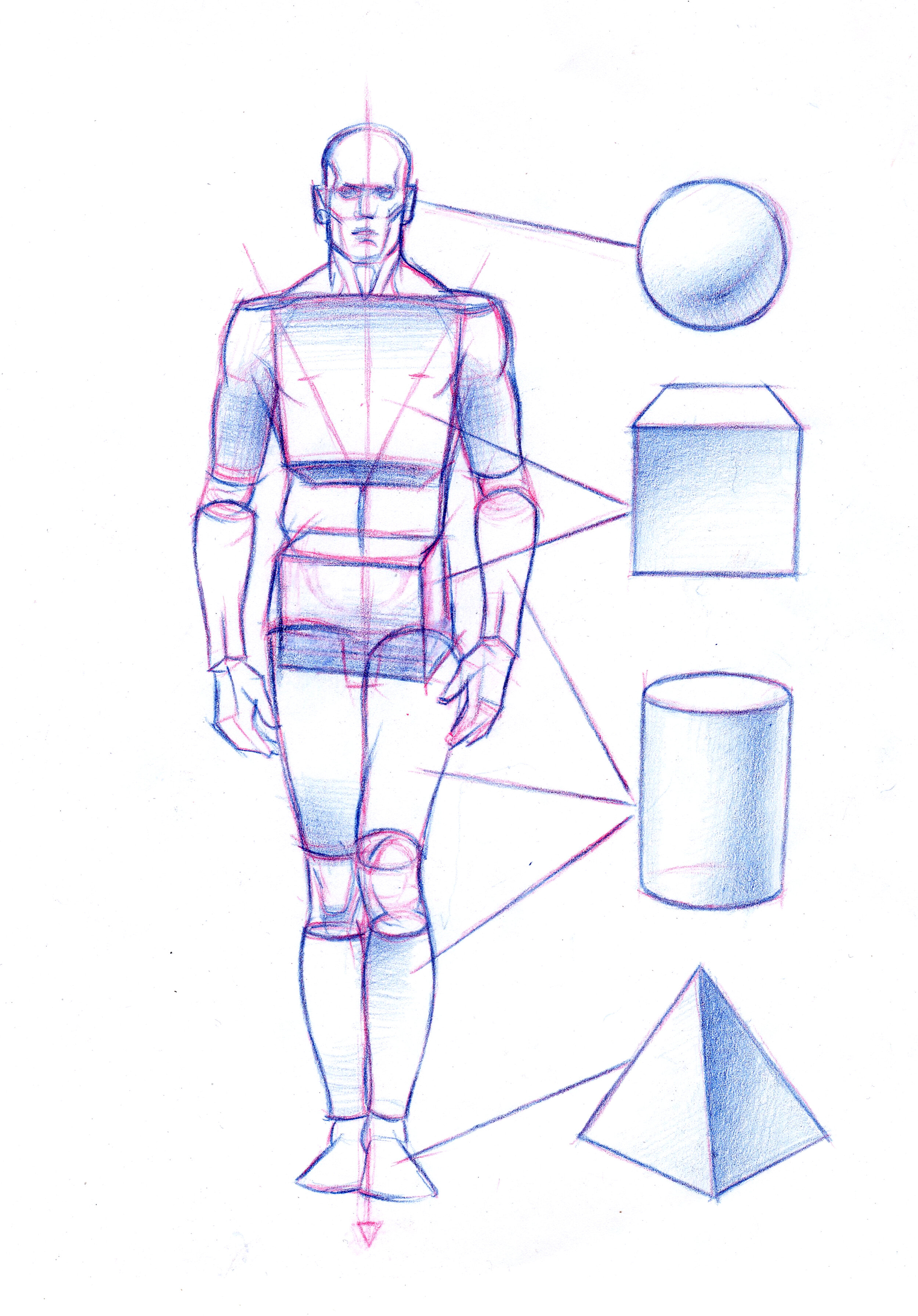
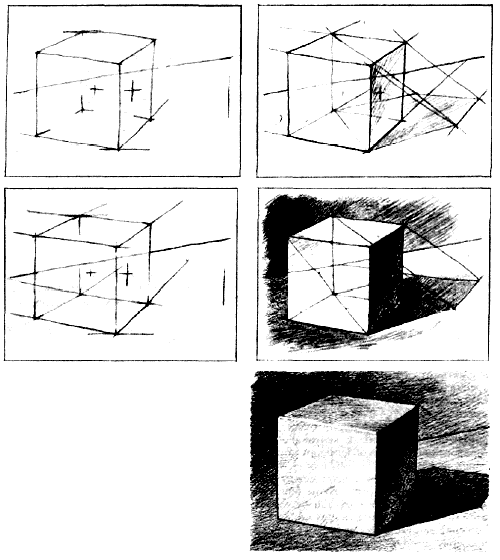
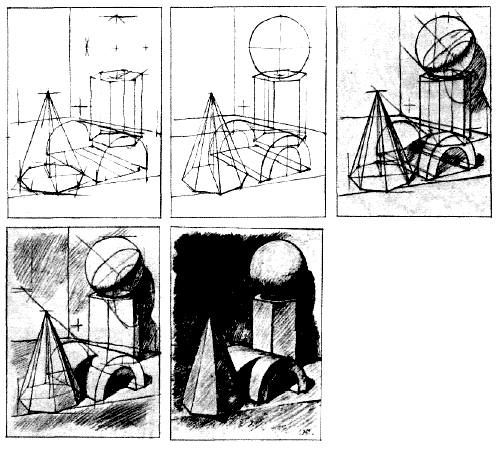
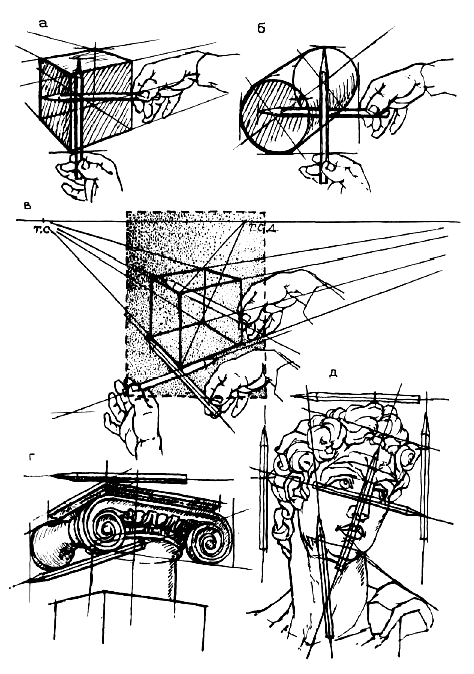
Продолжая рассматривать принципы построения конструкции объемных тел, необходимо ознакомиться с изображением геометрических форм гранных предметов (трехгранная и шестигранная призмы).

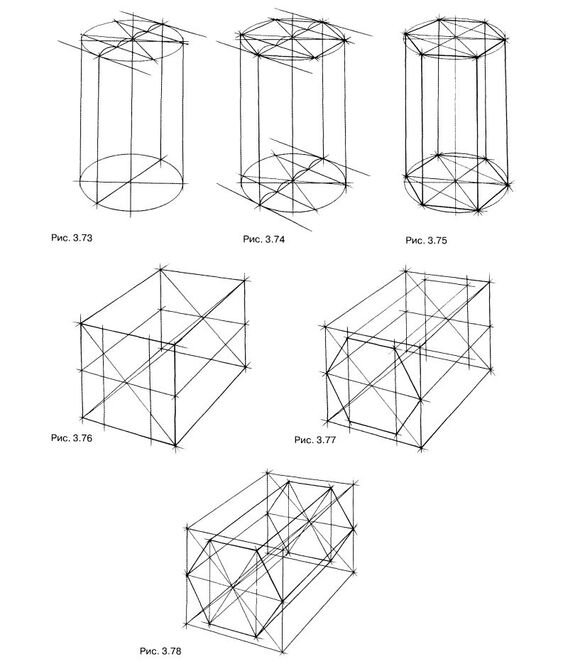
Трехгранная призма характеризуется шестью точками пространственных углов оснований и тремя линиями ребер. Ось призмы определяется линиями, проведенными от пространственных углов оснований перпендикулярно к ее противоположным сторонам. Из точек их пересечения проводят вертикальную линию, которая и будет осью призмы. При построении трехгранной призмы необходимо правильно выбрать точку зрения. Предмет должен быть изображен таким образом, чтобы он выглядел трехмерным, с двумя видимыми плоскостями и передним ребром, несколько смещенным в сторону. Трехгранная призма при таком повороте будет наиболее выразительна, объемна и целесообразна при условии, что предмет расположен в оптимальном перспективном ракурсе.

Большие трудности испытывают студенты при определении величин отрезков граней в перспективном ракурсе на основании призмы. Чтобы избежать ошибок, рекомендуется использовать дополнительную окружность (в плане, вид сверху), на которой, в соответствии с видимым положением предмета, точно определяются пространственные углы основания призмы. Таким образом, для правильного изображения призматических форм необходимо построить цилиндрическую схему с последующим построением в ней гранных форм.

Рис. 39-41

Построение трехгранной призмы следует начинать с проведения горизонтальной линии (она должна быть проведена строго горизонтально). Это дает возможность правильно определить положение поверхности оснований призмы по отношению к оси тела. После чего следует провести вертикальную осевую линию. Отмечая радиус основания, нарисовать окружность (эллипс) в перспективном ракурсе (рис.39). Для правильного определения пространственных точек углов основания на эллипсе необходимо над ним, в соответствии с радиусом эллипса, по одной оси нарисовать круг. Рисуя его, проверить, насколько правильно он нарисован, так как на искаженном круге невозможно будет точно определить пространственные точки и величины отрезков граней. От того, как верно они определены на круге, во многом будет зависеть правильность изображения поверхности основания призмы и всего предмета в целом.

Точно определив на круге видимое положение точек пространственных углов основания призмы, перенесите их на эллипс. Для определения ее верхнего, основания следует повторить рисунок эллипса, после чего, соединяя вертикальными линиями ребер пространственные точки оснований, получают построение изображения трехгранной призмы. На перспективном изображении призмы окружность (эллипс) нижнего основания должна быть несколько шире верхней.

Производя построение предмета на плоскости, следует строго соблюдать пропорции и перспективу. Для большей выразительности ее объемно-пространственной характеристики следует выделить ближние края формы более контрастными линиями, ослабляя и смягчая их по мере удаления. Во время продолжительного, многочасового занятия рисунком можно постепенно избавиться от всех вспомогательных линий. Рисунок в процессе построения следует выполнять легким нажимом карандаша на бумагу, с тем, чтобы по мере уточнения изображения можно было корректировать и удалять ненужное.

Шестигранная призма характеризуется двенадцатью точками пространственных углов основания и шестью линиями ребер. Ее ось определяется линиями, проведенными от противоположных пространственных углов основания, где точка их пересечения будет центром, через который проходит ось призмы. Для правильного определения ее пространственных углов, так же, как и при построении трехгранной призмы, необходимо начинать работу с построения эллипса и окружности под ним. В соответствии с видимым положением предмета при данной точке зрения следует правильно определить на окружности точки пространственных углов правильного шестигранника. Необходимо обратить внимание на поворот призмы, не следует рисовать шестигранную призму при симметричном расположении ее плоскостей. Поэтому при выборе места рисования нужно сесть так, чтобы предмет выглядел наиболее выразительно, объемно, как, например, показано на рис.40.

Перспективное построение шестигранной призмы производят тем же способом, как и при изображении трехгранной призмы. Сложность состоит в правильном определении с видимого положения перспективно сокращенных граней, их пропорциональных отношений. В этом случае также следует пользоваться вспомогательной окружностью в плане у нижнего основания призмы, как показано на рис.40. Построив окружность основания призмы, нужно определить шесть пространственных углов по окружности. При этом важно правильно отложить равные отрезки с учетом поворота призмы, т.е. с видимого положения. Соединяя точки легкими линиями, необходимо проследить за параллельностью противоположных сторон. Получив точки пространственных углов основания, так же, как и в первом случае, следует перенести их на нижнее основание эллипса. Необходимо отметить, что при переносе пространственных углов на основание эллипса учитывают перспективное сокращение его дальней половины, хотя эти изменения и несущественны. Главное, не допустить обратной перспективы.

Соединив линиями все точки на основаниях, приступают к проверке выполненных работ. Замеченные ошибки, не откладывая, исправляют. В целях достижения наибольшей выразительности изображения пространственной формы нужно ближние вертикальные и горизонтальные линии ребер усилить, а дальние - ослабить. При необходимости продолжения работы над рисунком следует избавиться от вспомогательных линий построения при помощи ластика.

Трехгранная пирамида (рис.41) характеризуется тремя точками пространственных углов основания, точкой вершины и шестью линиями ребер.

Для правильного изображения пирамиды рисунок следует начинать с построения ее основания, что аналогично построению призматической формы. Соединив точки пространственных углов основания линиями, необходимо найти конструктивную ось пирамиды и точку ее вершины.

Положение конструктивной оси определяется линиями, проведенными от пространственных углов основания перпендикулярно к его сторонам. От точки пересечения проводят вертикальную линию. Затем необходимо определить положение точки вершины пирамиды на осевой линии, что осуществляется в соответствии с пропорциональной величиной высоты натурной модели. После чего следует соединить вершину с пространственными углами основания.

Рис. 42-43

Четырехгранная пирамида (рис.42), в отличие от трехгранной, характеризуется четырьмя точками пространственных углов основания, точкой вершины и восемью линиями ребер. Конструктивная ось пирамиды, аналогично трехгранной, определяется соединением линиями их противоположных пространственных углов. Из точки пересечения проводят вертикальную (осевую) линию, на которой должна быть обозначена точка вершины пирамиды.

При построении пирамиды в горизонтальном положении следует обратить внимание на положение оси пирамиды по отношению к центру ее основания (рис. 43). При этом плоскость основания пирамиды по отношению к ее конструктивной оси должна находиться строго под прямым углом, то есть перпендикулярно, независимо от положения предмета при данной точке зрения. Структура строения тела также остается неизменной.

Хотите начать обучение?

Свяжитесь с нами!

Записаться также можно по тел.: 054 344 9543
https://www.ghenadiesontu.com/workshops/

Рисование геометрических тел. Как нарисовать куб?

Куб является одним из самых простых геометрических тел. Чтобы лучше понять геометрическую форму куба, его пространственную конструктивную схему (структуру), рассмотрим каркас куба. Это дает возможность ясно представить объемно-пространственную характеристику его формы, позволяет видеть его конструктивные узлы - точки, невидимые на обычных телах.

Рис.35

Куб характеризуется восемью точками на углах и двенадцатью линиями ребер. Соотношения сторон куба составляют пропорцию 1:1:1. Для того чтобы куб выглядел достоверно в трехмерном изображении, студентам следует определить такую точку зрения, при которой предмет выглядит достаточно убедительным в объеме. Изображение каркаса куба производится с учетом его пропорций, по законам перспективы. При обычном взгляде сверху (в ракурсе) основание каркаса куба (квадрат) выглядит ромбом. Перспективное построение куба в соответствии с его поворотом следует начинать с квадрата основания, т.е. с его плана, лежащего в горизонтальной плоскости, уходящей в глубину до линии горизонта (рис.35). Чтобы получить нижнее основание (ромб), необходимо обозначить четыре точки и соединить их четырьмя линиями. Из точек основания проводят вертикальные линии - ребра. Для завершения построения, как и в первом случае, обозначают четыре точки и, соединив их четырьмя линиями, получают верхнее основание куба (ромб). Необходимо отметить одну немаловажную деталь, касающуюся характера линий при построении изображения на плоскости. Кроме соблюдения пропорции и перспективы, линии, определяющие пространственную глубину, должны быть проведены в различной степени контрастности. Линии близлежащих ребер следует проводить более контрастно, чем тех, что находятся в перспективном удалении. Причем разница линий должна быть предельно различимой в соответствии с пространственной глубиной.

Рис.36. Измерение пропорциональных величин

Перспективный рисунок куба может быть сравнительно легко построен и проверен различными способами. Одним из таких способов являются приемы, давно применяемые на практике старыми мастерами, - это сравнение и визирование. Для определения основных больших размеров предмета в рисунке важны видимые, перспективно измененные их соотношения, а не реальные размеры объекта и его частей. Так, например, отношение ширины какой-либо грани к высоте переднего ребра вымеряют карандашом на вытянутой руке, перпендикулярно лучу зрения, совмещая тыльную сторону карандаша с краем формы предмета измеряемой части модели. При этом большим пальцем отмечают видимые размеры частей предмета. Не меняя положения большого пальца на вытянутой руке и поворачивая карандаш в вертикальном положении, соотносят этот отрезок карандаша с вертикальным ребром куба, определяя визуально их различия (рис.36).

Работая над конструктивным построением куба, нужно внимательно следить за его перспективным сокращением. Для этого необходимо мысленно представить форму с данной точки зрения в плане, т.е. увидеть ее сверху. Такое представление дает возможность лучше разобраться, как согласуются плоскости между собой и в целом. В рисовании с натуры важно правильно передать не только видимые соотношения величин, но и величины углов между основаниями двух видимых граней, т.е. перспективные ракурсы.

Для их правильного определения следует сделать проверку механическим способом визирования. Держа карандаш за кончик на вытянутой руке, нужно совместить линию самого карандаша с вершиной переднего нижнего угла основания предмета и определить на глаз угол наклона предмета в перспективе. Запомнив увиденное, проведите на своем рисунке соответствующую вспомогательную горизонтальную линию. Сравнивая величину наклона (угла) правой и левой сторон модели, уточните рисунок. При необходимости дополнительного уточнения следует повторить проверку. На рис.36 наглядно показаны способы измерения размеров и проверки перспективного наклона горизонтальных ребер куба. Заметим, что, рисуя с натуры, не нужно злоупотреблять приемом визирования, поскольку он носит чисто механический характер определения размеров и не способствует развитию глазомера. Им пользуются на начальной стадии обучения рисованию с натуры, и он должен служить лишь для вспомогательного контроля и проверки уже выполненных работ.

При положении куба со смещенным несколько вправо от центра передним вертикальным ребром горизонтальные ребра его левой грани в перспективе будут приближаться к горизонтали, а ребра правой, наоборот - отклоняться от нее. Следовательно, чем больше сокращается правая грань, тем меньше будет сокращение левой и наоборот. Это обусловлено взаимным прямоугольным расположением плоскостей куба.

Для лучшего усвоения материала по изучению геометрических тел необходимо выполнить академическое задание по рисунку куба. Усваивая закономерности строения формы куба, следует иметь в виду, что за их соблюдением нужно следить на протяжении всего процесса рисования с натуры. Работа над длительным рисунком требует соблюдения методической последовательности как в анализе строения формы, так и в процессе построения изображения. Это дает возможность закреплять отдельные этапы учебного рисунка, без чего невозможно понять основной смысл учебного материала. При этом следует отметить, что членение процесса работы над рисунком на отдельные этапы носит достаточно условный характер. Это связано с ошибками в решении задач, которые могли быть допущены на предыдущем этапе, и необходимостью их исправления в процессе работы.

Рис.37. Последовательность работы над рисунком куба

Рассмотрим последовательность выполнения рисунка куба (рис.37).

1. Рисунок начинают с композиционного размещения предмета на листе. Изображение намечают легкими линиями с боков, сверху и снизу. С учетом ракурса, пропорции и перспективы находят и определяют основные конструктивные точки вершин углов куба.
2. С учетом перспективных сокращений по конструктивным точкам вершин углов намечают общую форму конструкции куба.
3. Уточняют пропорции и перспективное построение объемно-пространственной формы куба. Определяют границы собственной и падающей теней.
4. С помощью светотональных отношений выявляют объемную форму куба. Наносят собственные и падающие тени. Определяют фон.
5. Полная тональная проработка формы. Работа светотональными отношениями: свет, тень, полутень и рефлекс.
6. Подведение итогов. .Проверка и обобщение рисунка (цельность).

Рис. 38. Перспективное построение куба

Форма, объем, конструкция

Для того чтобы научиться верно изображать предметы с натуры на плоскости, необходимо иметь представление об их форме, объеме и конструкции. Эти сведения помогут в дальнейшем решать учебные задачи при работе над рисунком, позволят лучше понять и разобраться в строении предметных форм при изображении. В противном случае студенты могут перейти к механическому и бездумному копированию натурных предметов.

Главная задача при обучении рисунку - научиться правильно видеть объемную форму предмета и уметь ее логически последовательно изображать на плоскости листа бумаги. Для этого рассмотрим более детально строение предметов. В физической природе невозможно представить какое-либо тело, имеющее абстрактную форму, например пустоту. Не отвлекаясь на подобного рода объекты, перейдем к предметам реальным, окружающим нас повсюду, включая формы живой натуры. Под формой предмета следует понимать геометрическую сущность поверхности предмета, характеризующую его внешний вид.

Всякий предмет или объект в природе, от микрочастиц до гигантских космических тел, имеет определенную форму, и форма человеческого тела здесь не исключение. Следовательно, любой предмет есть форма, а форма подразумевает объем. Эти два понятия - форма и объем - неразрывно взаимосвязаны, составляют единое целое и раздельно в природе не существуют.

Для примера возьмем плоский предмет - лист бумаги, внешний вид которого характеризуют плоские очертания прямоугольной или обрывистой формы. Его объем будет определяться толщиной сечения, каким бы оно ни было тонким. Разумеется, этот пример применительно к рассматриваемой конкретной теме не совсем удачен. Было бы лучше, если бы лист бумаги был скомкан или ему была бы придана другая объемная форма. В этом случае предмет выглядел бы более выразительно. Возьмем книгу, внешние очертания которой при первоначальном рассмотрении имеют ту же форму, что и лист бумаги. Однако толщина книги вместе с общей площадью создают ее объем, делая этот пример более наглядным. Объем предмета - это трехмерная величина, которая ограничена в пространстве различными по форме поверхностями (любые предметы имеют высоту, ширину и длину, даже в относительном их измерении).

Форма любого предмета в своей основе понимается или рассматривается как его геометрическая сущность, его внешний вид или внешние очертания. Известный художник и педагог Д.Н.Кардовский считал, что форма есть масса, имеющая тот или иной характер подобно геометрическим телам, таким как куб, шар, цилиндр и др. Это в равной степени относится и к живым формам, которые при всей сложности имеют в основе (схеме) скрытую геометрическую сущность.

Так, например, форма туловища человека может быть представлена в виде нескольких геометрических форм: цилиндра, параллелепипеда или более приближенной к форме туловища уплощенной призмы. Однако четких очертаний названные геометрические формы в туловище человека не имеют, в нем присутствуют углубления, выступы и другие отклонения, которые мешают неискушенным рисовальщикам увидеть эти геометрические тела в живой форме.

Тем не менее, при внимательном анализе форм туловища просматривается его геометрическая сущность, которая приближена к форме призмы. Применяя эти геометрические формы при построении фигуры человека, конкретизируя и обобщая имеющиеся отклонения, можно придать фигуре реальные очертания.

Осмысливая внешние очертания предметов, необходимо также осмыслить и сущность их внутреннего строения, конструкцию формы и связь отдельных элементов, составляющих ту или иную форму. Конструкция предмета, как правило, определяет характер его формы. В учебном рисунке понятие конструкции формы приобретает особое значение с точки зрения ее пространственной организации, геометрической структуры, внешнего пластического строения, материала и ее функционального назначения. Это позволяет студентам более осознанно подходить к работе над рисунком.

При внимательном анализе форм предметов, при всей их кажущейся сложности, в них всегда можно увидеть геометрическую конструктивную основу или сочетание нескольких таких основ, образующих эту форму. Для примера возьмем кувшин, в основе которого можно выделить не-сколько различных по форме геометрических тел в следующем сочетании: горловина - цилиндр, корпус - шар, основание - конус. Конструктивная форма двухэтажного дома - прямоугольник, его крыша - трехгранная призма.

Геометрическая основа конструкции простых предметов очевидна, сложнее разглядеть ее в живых формах. Сложные формы также имеют скрытую геометрическую основу, что значительно упрощает понимание структурной и конструктивной сущности этих предметов. От структуры строения предмета во многом зависят приемы построения его формы на плоскости.

Поэтому, анализируя форму предмета, как бы она ни была сложна на первый взгляд, прежде всего необходимо проникнуть в сущность его внутреннего строения, не отвлекаясь на мелкие детали, мешающие понять геометрическую основу его конструкции. Это позволит студентам получить более полную информацию о предмете и осознанно выполнить рисунок. Только после этого можно приступить к решению изобразительных задач и свободно, уверенно рисовать как с натуры, так и по воображению, что чрезвычайно важно для профессиональной творческой деятельности.

Объемно-пространственное и конструктивное построение форм предметов

Традиционный метод построения изображений в классических восточных школах

Для лучшего понимания конструкции предметов и приобретения навыков грамотного изображения их формы также необходимо вспомнить полученные в школе знания по геометрии, такие, как понятия о точках, линиях и объемных формах.

Рисование геометрических тел

Главная задача учебного рисунка — изучение и практическое рисование с натуры многообразных форм, созданных природой и человеком. Рисуя с натуры какой-либо конкретный предмет, нужно постоянно возвращаться к повторению общих понятий и принципов учебного рисунка, чтобы они твердо вошли в сознание и в конце концов применялись бы при рисовании автоматически, без лишней затраты времени, без лишних физических и умственных усилий.
Практическая часть пособия построена по принципу последовательного возрастания трудности заданий: от рисования простых геометрических тел до работы над такими сложными по внутреннему строению и внешней пластике формами, как человек и архитектура. Освоение принципов рисунка, его технического и графического исполнения осуществляется сначала на простых формах геометрических тел и предметов быта, для рисования которых достаточно представления о внешнем облике, а затем на голове и фигуре человека, в изображении которых решающую роль играет знание внутренней конструкции и умение увидеть связь анатомического строения с внешней формой.
Эти упражнения являются достаточно хорошей школой для приобретения необходимых основ мышления и навыков в рисунке, владея которыми можно решать любые задачи, в том числе и рисования архитектурных сооружений. Опираясь на общие принципы, практическая часть пособия показывает применение единого метода в изучении и рисовании различных форм.
Методические таблицы на примерах конкретных форм и определенных задач иллюстрируют стадии практического ведения рисунка — от композиционного размещения и линейного построения до тонального решения.
Последовательность выполнения учебного рисунка на листе бумаги такова:

• пометка композиционного размещения крайними точками;

• нахождение геометрического центра композиции, от которого должно идти дальнейшее построение;

• пометка точками основных конструктивных узлов с учетом пропорций и перспективы и нанесение линиями направлений движения основных масс;

• прорисовка линиями больших форм с последующей дорисовкой деталей;

• нанесение светотени, начиная с линий собственных теней, проработки теней и кончая моделировкой формы на свету;

• обобщение и придание цельности рисунку.
  

  На каждой стадии работы необходима строгая проверка и исправление ошибок, допущенных в предыдущих стадиях.
  В методических таблицах проведен принцип применения минимума средств для решения той или иной задачи и разумного использования точек, линий и тушевки, различной их силы в начале, середине и конце выполнения работы.
  

  Прежде чем приступить к выполнению рисунка, поставить первую точку и провести первую линию, нужно осознать, что и для чего делать и в какой последовательности во времени вести работу. Необходимо учитывать, что человек не может сразу ответить на все вопросы правильно, ему свойственно ошибаться, поэтому манера в начале работы должна быть такой, которая обеспечивает возможность ясно видеть ошибки и исправлять их с минимальной затратой времени и усилий. Последнее достигается использованием в рисунке точек и линий различной силы.
  Первые пометки на листе бумаги в учебном рисунке как с натуры, так и по представлению должны быть слабыми, скупыми или, как говорят, исчезающими, а после анализа и сравнения с натурой исправления следует вносить более сильной линией. Первые пометки по контрасту с последующими при этом становятся незаметными, а к резинке при такой манере учебного рисунка приходится прибегать крайне редко — тогда, когда ошибочная пометка сделана настолько сильно, что спорит с правильной и мешает видеть рисунок. Стирать ошибочные пометки рекомендуется только после того, как найдены правильные.
  Большое значение имеют кратковременные рисунки с натуры и по представлению. Поэтому перед тем, как делать длительный учебный рисунок с той или другой точки зрения, рекомендуется осмотреть рисуемый предмет-модель со всех сторон и сделать с характерных точек кратковременные рисунки-наброски, как правило, линейные, позволяющие полнее изучить рисуемую форму в целом, более уверенно и успешно вести длительный рисунок с нее. С помощью набросков можно получить ясное представление о внешней форме, о движении в пространстве и о пропорциях рисуемого объекта. Если форма предмета сложная, то для ясного ее понимания полезно сделать мысленно ряд сечений плоскостью и изобразить эти сечения на бумаге линией. Иногда быстрый набросок может решать одну из частных задач рисунка: в одном случае — конструктивную, в другом — задачу пропорций и передачи характера, в третьем — движения, светотени или композиции. Для решения каждой из задач следует выбирать соответствующую манеру изображения и степень законченности.

Рис 1. Последовательность рисунка куба

Так, ниже, на рис. 1 - 5, где показана последовательность ведения рисунка, вторая стадия может служить примером учебного наброска, решающего задачи композиционного размещения, движения и пропорций основных масс; третья — уточнения пропорций, конструктивного и перспективного построения; четвертая стадия — общего светотеневого решения.

Рис 2. Последовательность рисунка цилиндра

При рисовании с натуры можно рекомендовать ряд механических приемов определения основных больших размеров и направлений, позволяющих избежать, особенно вначале, грубых ошибок в размерах, движении и перспективе. На рис. 6, 7 показан способ измерения видимых с данной точки линейных размеров натуры и сравнения их в рисунке при помощи карандаша. Карандаш помещается между глазом и натурой и на нем пальцем отмечаются видимые размеры частей натуры. Следует помнить, что карандаш нужно держать строго перпендикулярно лучу зрения и на одинаковом расстоянии от глаза, лучше всего на расстоянии вытянутой руки.

Рис 3. Последовательность рисунка шара

Так как движение принято рассматривать по отношению к вертикали или горизонтали, то для облегчения определения наклона всей формы или ее части полезно поместить карандаш между глазом и натурой в вертикальном положении и сравнить с ним наклон основных осей и линий формы, а также расположение ее отдельных частей. Такую же проверку следует провести в горизонтальном направлении. На рис. 6,в показано, как при помощи карандаша можно облегчить нахождение точек схода для ребер куба на картинной плоскости. Следует помнить, однако, что указанные и другие механические способы не могут заменить корректирующую роль сознания при оценке правильности изображения в учебном рисунке и тем более в рисунке, решающем творческие задачи.

Рис 4. Последовательность рисунка конусов

Наряду с перспективными рисунками, сделанными с одной точки, для изучения конструктивного построения и истинных пропорций предмета необходимо рисовать основные его виды с разных сторон — сверху, спереди, сзади, снизу, справа, слева методом ортогональных проекций.

Рис 5. Последовательность рисунка натюрморта из геометрических тел

В тех случаях, когда конструкция и пластическая форма предмета достаточно сложны, полезно мысленно представить ряд характерных разрезов, а также нарисовать их ортогональные изображения. Такой метод сопоставления перспективного изображения предмета с ортогональными проекциями основных видов и с характерными сечениями способствует, во-первых, лучшему изучению рисуемого предмета и, вовторых, развитию объемно-пространственного мышления, которое обеспечивает более убедительное изображение предмета на плоскости не только с натуры, но, что особенно важно для архитектора, по воображению.
Чувство взаимной связи реального пространства и формы в натуре с их изображениями в виде плана, фасада, разрезов и перспективы особенно необходимо архитектору, который в своей творческой практике должен иметь общие представления об образе сооружения приводить к плану, фасаду и разрезам, а по ортогональным изображениям представлять внешний вид будущего сооружения с разных точек зрения.
После изучения и рисования предмета с натуры рекомендуется нарисовать его по памяти в разных положениях.
Для закрепления знаний о светотени целесообразно нарисовать предмет с натуры в линиях, а тени нанести без натуры, по представлению, задавшись определенным положением источника света в пространстве. Для последующей проверки следует поместить источник света в задуманное место и сравнить рисунок с натурой.
Объем пособия позволяет разобрать лишь ограниченное число примеров методики рисования. Для более углубленного изучения бесконечного богатства и разнообразия форм природы, их конструкции, пластики и окружающих их условий необходимо рисовать приведенные в пособии предметы, разнообразя их повороты и освещение, а также расширить круг упражнений рисованием любых других предметов, что существенно дополнит и обогатит познания и умение учащегося.

Рис 6. Механический прием определения основных размеров и направлений на натуре

Школа конструктивного рисования основывается на последовательности обучения — от простого к сложному. Освоение принципов рисунка лучше всего начинать с упражнений в рисовании простых пространственных форм. Для этой цели больше всего подходят геометрические тела, имеющие ясное конструктивное построение. На них легче всего проследить, понять и усвоить основы пространственного построения конструкции, перспективного ее изображения и закономерностей светотени. Внимание рисующего целиком сосредоточивается на главных элементах грамоты рисования, он не отвлекается на многообразие задач, связанных с рисованием более сложных форм, таких, как тело человека или архитектура. Закономерности, понятые и усвоенные при рисовании простых форм, помогают затем в изучении более сложных форм и осознанном их изображении.
Рисование геометрических форм имеет непосредственное практическое значение, так как в своей деятельности архитектор использует формы, близкие, как правило, к геометрическим. Такие базовые геометрические тела, как куб, призма, пирамида, конус, цилиндр и шар, наиболее часто употребляются в учебном рисовании.
Учащийся сам может изготовить из проволоки, деревянных реечек, листа ватмана, картона или пенопласта простейшие геометрические тела. Размеры тел должны быть взяты в пределах 15—20 см. Хорошо сделать каркасы простых геометрических тел из проволоки или деревянных реек (куб, призмы, пирамиды и т. д.). Конструктивные узлы в проволочных моделях могут быть соединены при помощи пайки или деревянных шариков с просверленными отверстиями. Деревянные рейки можно склеить, укрепив дополнительно накладками из жести.
«Прозрачность» каркасных моделей позволяет видеть сразу все основные узлы их конструкции, невидимые на обычных предметах. Это в значительной степени облегчает построение рисунка: рисующий ясно понимает, как располагаются в пространстве «видимые» и «невидимые» углы, ребра и грани тела в различных поворотах. Рисование каркасов уже в начале обучения помогает развитию объемно-пространственного мышления.
В дальнейшей работе для усвоения закономерностей распределения светотени следует использовать модели, сделанные из листа ватмана или картона: куб, призмы и пирамиды с различным числом граней, цилиндр и конус. Для этого необходимо вычертить соответствующие развертки, вырезать их и, согнув должным образом, склеить.

Рис 7. Механический прием определения основных размеров на натуре

Поворачивая эти тела по отношению к точке зрения и к источнику света, ставя их в несложных комбинациях друг с другом, можно получить целый ряд интересных для рисования постановок, охватывающих все принципиальные задачи конструктивного рисунка: построение конструкции, пропорции, закономерности перспективы и светотени и тональные отношения.
Сам процесс, при котором учащийся своими руками изготовляет объемный предмет и затем рисует его на листе бумаги, в значительной мере помогает осознать строение формы, особенности ее видения и изображения.
Рассмотрим изображения куба с полной светотеневой проработкой и сновные" последовательные стадии его рисования (рис. 1).
1-я стадия — пометка композиционного размещения на листе крайними точками, определение центра размещения изображения и нахождение основных точек вершин углов куба с учетом движения, пропорций и перспективы при данной точке зрения.
2-я стадия — прорисовка конструкций куба легкими тонкими линиями по помеченным узловым пунктам с учетом горизонта и точек схода.
3-я стадия — уточнение пропорций и перспективного построения более сильными линиями. Нахождение характерных пунктов собственной тени и определение соответствующих им пунктов падающей тени.
4-я стадия — решение больших тональных отношений: нанесение собственной тени, падающей тени и определение фона.
5-я стадия — полная тональная проработка всего рисунка: передача отношений в тенях и светах до выявления рефлексов и бликов; нахождение обобщающих тональных отношений для придания цельности рисунку.
Такая же последовательность стадий и при рисовании цилиндра (рис. 2), шара (рис. 3) соответственно с полной светотеневой проработкой.
Рисование геометрических тел, проиллюстрированное рис. 4, 5, основано на тех же принципах и последовательности и может быть усвоено без дополнительного описания. Следует лишь напомнить, что при практическом учебном рисовании с натуры для приобретения твердых знаний и навыков нужно постоянно обращаться к теоретической части различных пособий по архитектурному рисунку, в которых даны понятия о конструкции, движении, пропорциях, перспективе, светотени и композиции.