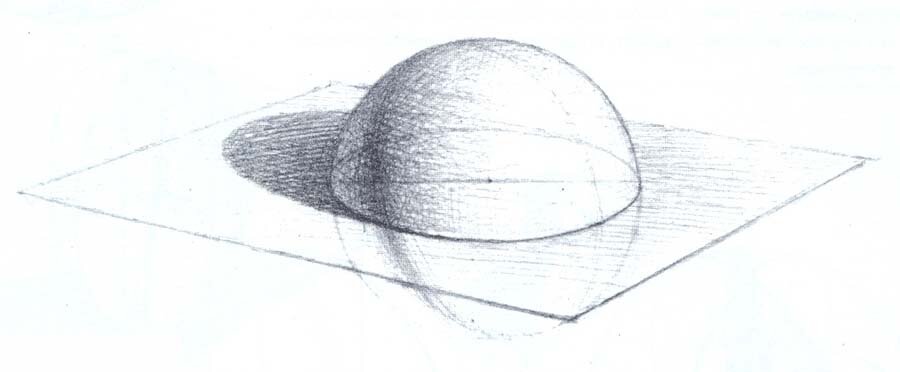
Шар имеет замкнутую сферическую поверхность, особенность строения которой заключается в том, что все ее конструктивные точки находятся на равном удалении от центра (рис.55). Таким образом, поверхность шара рассматривается как форма, образованная вращением окружностей (образующих) вокруг оси (диаметра).
Линейно-конструктивное построение шара не представляет особой сложности, значительно сложнее выявить его форму светотенью. На рис.55 наглядно показаны приемы и методы построения шара с двумя и более образующими, поэтому останавливаться на них нет необходимости.
Рис.55
Для построения достаточно ограничиться двумя-тремя пересекающимися образующими. Отложив от центра радиусы шара, проводят замкнутую кривую - контур шара, после чего можно приступить к лепке его формы светотенью, удалив предварительно вспомогательные линии построения.
Рис.56
Сложность объемного построения шара тоном связана с богатством светотеневых колебаний (градаций светотени) на его поверхности по сравнению с другими телами, что обусловлено не только характером сферической поверхности, но одновременно и степенью освещенности. Освещенная поверхность постепенно убывает, огибая круг, переходя от света к тени - к увеличивающимся границам собственных теней и на затененный участок шара, где тон постепенно высветляется рефлексом и мягко переходит из одной тональности в другую - к падающей тени. Падающая тень темнее собственной, особенно у его основан
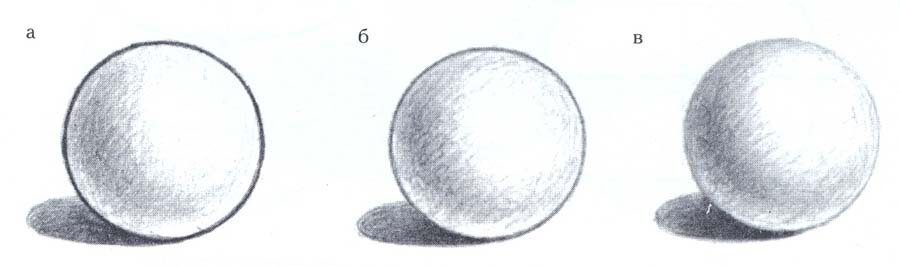
Рис.57
Сложность при передаче формы шара светотенью возникает в процессе выявления тональных отношений между его контуром и фоном, т.е. при создании иллюзии объемности. Контуры шара на видимом фоне должны быть нарисованы мягко и убедительно, чтобы края формы не вырывались из глубины пространства, а вызывали впечатление ее закругленности. В качестве примера приведены изображения формы шара (рис.57). Все шары выполнены в тоне в равной степени, однако воспринимаются различно. У шаров (рис.57, а,б) чрезмерно усилены края формы, на рис.57,в - края формы умеренно подчинены ей.
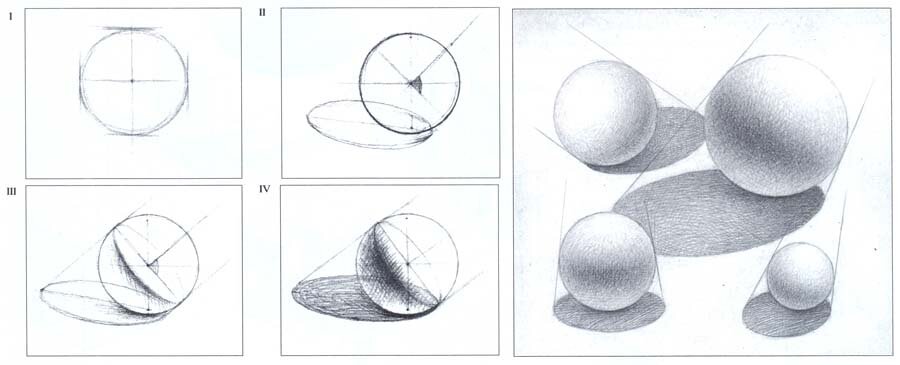
Рис.58. Этапы построения шара
Чтобы научиться правильно работать светотенью, необходимо знать закономерности ее распределения. Изучив эти законы на простых геометрических телах, можно разобраться в светотенях любых сложных по форме предметов. В связи с чем нам следует перейти к их рассмотрению.